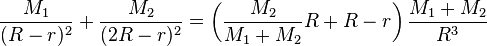![poker]()
This post is based on the fantastic PlusMaths article on bluffing- which is a great introduction to this topic. If you’re interested then it’s well worth a read. This topic shows the power of mathematics in solving real world problems – and combines a wide variety of ideas and methods – probability, Game Theory, calculus, psychology and graphical analysis.
You would probably expect that there is no underlying mathematical strategy for good bluffing in poker – indeed that a good bluffing strategy would be completely random so that other players are unable to spot when a bluff occurs. However it turns out that this is not the case.
As explained by John Billingham in the PlusMaths article, when considering this topic it helps to really simplify things first. So rather than a full poker game we instead consider a game with only 2 players and only 3 cards in the deck (1 Ace, 1 King, 1 Queen).
The game then plays as follows:
1) Both players pay an initial £1 into the pot.
2) The cards are dealt – with each player receiving 1 card.
3) Player 1 looks at his card and can:
(a) check
(b) bet an additional £1
4) Player 2 then can respond:
a) If Player 1 has checked, Player 2 must also check. This means both cards are turned over and the highest card wins.
b) If Player 1 has bet £1 then Player 2 can either match (call) that £1 bet or fold. If the bets are matched then the cards are turned over and the highest card wins.
So, given this game what should the optimal strategy be for Player 1? An Ace will always win a showdown, and a Queen always lose – but if you have a Queen and bet, then your opponent who may only have a King might decide to fold thinking you actually have an Ace.
In fact the optimal strategy makes use of Game Theory – which can mathematically work out exactly how often you should bluff:
![poker2]()
This tree diagram represents all the possible outcomes of the game. The first branch at the top represents the 3 possible cards that Player 2 can be dealt (A,K,Q) each of which have a probability of 1/3. The second branch represents the remaining 2 possible cards that Player 1 has – each with probability 1/2. The numbers at the bottom of the branches represent the potential gain or loss from betting strategies for Player 2 – this is calculated by comparing the profit/loss relative to if both players had simply shown their cards at the beginning of the game.
For example, Player 2 has no way of winning any money with a Queen – and this is represented by the left branch £0, £0. Player 2 will always win with an Ace. If Player 1 has a Queen and bluffs then Player 2 will call the bet and so will have gained an additional £1 of his opponents money relative to a an initial game showdown (represented by the red branch). Player 1 will always check with a King (as were he to bet then Player 2 would always call with an Ace and fold with a Queen) and so the AK branch also has a £0 outcome relative to an initial showdown.
So, the only decisions the game boils down to are:
1) Should Player 1 bluff with a Queen? (Represented with a probability of b on the tree diagram )
2) Should Player 2 call with a King? (Represented with a probability of c on the tree diagram ).
Now it’s simply a case of adding the separate branches of the tree diagram to find the expected value for Player 2.
The right hand branch (for AQ and AK) for example gives:
1/3 . 1/2 . b . 1
1/3 . 1/2 . (1-b) . 0
1/3 . 1/2 . 0
So, working out all branches gives:
Expected Value for Player 2 = 0.5b(c-1/3) – c/6
Expected Value for Player 1 = -0.5b(c-1/3) + c/6
(Player 1′s Expected Value is simply the negative of Player 2′s. This is because if Player 2 wins £1 then Player 1 must have lost £1). The question is what value of b (Player 1 bluff) should be chosen by Player 1 to maximise his earnings? Equally, what is the value of c (Player 2 call) that maximises Player 2′s earnings?
It is possible to analyse these equations numerically to find the optimal values (this method is explained in the article), but it’s more mathematically interesting to investigate both the graphical and calculus methods.
Graphically we can solve this problem by creating 2 equations in 3D:
z = 0.5xy-x/6 – y/6
![poker7]()
z = -0.5xy+x/6 + y/6
![poker8]()
In both graphs we have a “saddle” shape – with the saddle point at x = 1/3 and y = 1/3. This can be calculated using Wolfram Alpha. At the saddle point we have what is known in Game Theory as a Nash equilibrium – it represents the best possible strategy for both players. Deviation away from this stationary point by one player allows the other player to increase their Expected Value.
Therefore the optimal strategy for Player 2 is calling with precisely c = 1/3 as this minimises his loses to -c/6 = -£1/18 per hand. The same logic looking at the Expected Value for Player 1 also gives b = 1/3 as an optimal strategy. Player 1 therefore has an expected value of +£1/18 per hand.
We can arrive at the same conclusion using calculus – and partial derivatives.
z = 0.5xy-x/6 – y/6
For this equation we find the partial derivative with respect to x (which simply means differentiating with respect to x and treating y as a constant):
zx = 0.5x – 1/6
and also the partial derivative with respect to y (differentiate with respect to y and treat x as a constant):
zy = 0.5y -1/6
We then set both of these equations to 0 and solve to find any stationary points.
0 = 0.5x – 1/6
0 = = 0.5y -1/6
x = 1/3 y = 1/3
We can then see that this is a saddle point by using the formula:
D = zxx . zyy – (zxy)2
(where zxx means the partial 2nd derivative with respect to x and zxy means the partial derivative with respect to x followed by the partial derivative with respect to y. When D < 0 then we have a saddle point).
This gives us:
D = 0.0 – (0.5)2 = -0.25
As D < 0 then we have a saddle point – and the optimal strategy for both players is c= 1/3 and b = 1/3.
We can change the rules of the game to see how this affects the strategy. For example, if the rules remain the same except that players now must place a £1.50 bet (with the initial £1 entry still intact) then we get the following equation:
Player 2 Expected Value = b/12(-1+7c) – 3c/12
This has a saddle point at b = 3/7, c = 1/7. So the optimal strategy is 3/7 bluffing and 1/7 calling. If Player 2 calls more than 3/7 then Player 1 can never bluff (b = 0), leaving Player 2 with a negative Expected Value. If Player 2 calls less than 3/7 then Player 1 can always bluff (b = 1).
If you enjoyed this you might also like:
The Gambler’s Fallacy and Casino Maths - using maths to better understand casino games
Game Theory and Tic Tac Toe - using game theory to understand games such as noughts and crosses
![]()















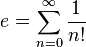
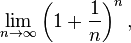
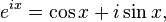






























![r \approx R \sqrt[3]{\frac{M_2}{3 M_1}}](http://upload.wikimedia.org/math/a/a/8/aa8238630357939a5327ec9f4eb7b3d4.png)